Aplicación de Jackknife en la determinación de intervalos de confianza para el coeficiente de variación

A continuación se muestra el código en R para la determinación de la varianza, sesgo e intervalos de confianza para el coeficiente de variación utilizando Jackknife:

### Paquetes ### 
library(nortest)

### Datos ###
datos <- c(13.0,10.8,12.7,14.2,10.5,11.3,15.7,19.8,16.2,20.3,9.9,21.4)

### Jackknife ###
n <- length(datos)
k <- 100

NOMBRES=NULL
i=1 
while(i<=k) 
{
  NOMBRES=c(NOMBRES,paste("M",i,sep=""))
  i=i+1
}
NOMBRES

TABLA=NULL
i=1
while(i<=k)
{
  muestra=sample(datos,(n-1),replace=TRUE)
  desvp=c((var(muestra)*(n-2)/(n-1))^(1/2))
  coefvar=c(muestra,desvp,(desvp/mean(muestra)))
  TABLA=rbind(TABLA, coefvar)
  i=i+1
}
colnames(TABLA)[ncol(TABLA)]="coefvar"
colnames(TABLA)[(ncol(TABLA)-1)]="desv_pob"
rownames(TABLA)=NOMBRES
TABLA
#View(TABLA)
coefvar <- TABLA[,ncol(TABLA)]
hist(coefvar, main="HISTOGRAMA DEL COEFICIENTE DE VARIACIÓN", freq=FALSE)
lines(density(coefvar), col="red", lwd=2)

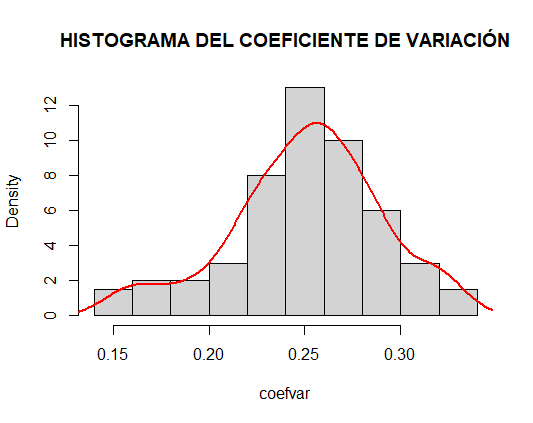lillie.test(coefvar)

Lilliefors (Kolmogorov-Smirnov) normality test

data:  coefvar
D = 0.064203, p-value = 0.3949

coefvar_datos=((var(datos)*(n-1)/(n))^(1/2))/mean(datos)
coefvar_datos

[1] 0.2644189

sesgo= mean(coefvar)-coefvar_datos
sesgo

[1] -0.01371688

varianza=(var(coefvar)*(k-1)/(k))
varianza

[1] 0.001526572

# IC usando las cuantilas muestrales
ICinf=c(quantile(coefvar, probs=0.025))
ICinf

 2.5% 
0.1583728

ICsup=c(quantile(coefvar, probs=0.975))
ICsup

    97.5% 
0.3210539 

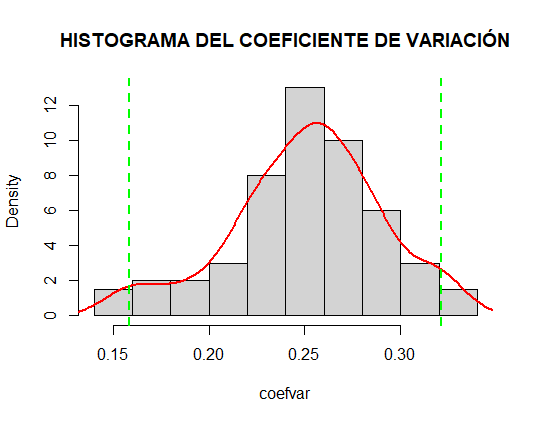
hist(coefvar, main="HISTOGRAMA DEL COEFICIENTE DE VARIACIÓN", freq=FALSE)
lines(density(coefvar), col="red", lwd=2)
abline(v=ICinf, col="green", lwd=2, lty = 2)
abline(v=ICsup, col="green", lwd=2, lty = 2)

Referencias

(1) HOLLANDER M., WOLFE D. A. y otro. Nonparametric Statistical Methods. Tercera edición. Wiley Series in Probability and Statistics. Páginas 420 - 427